Distance is defined by points ![]() and
and ![]() :
:
| (6.14) |
| (6.15) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
| (6.16) | |||
| (6.17) |
Angle is defined by points ![]() ,
, ![]() , and
, and ![]() , and spanned by vectors
, and spanned by vectors
![]() and
and ![]() :
:
| (6.18) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
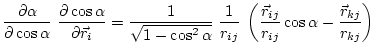 |
(6.19) | ||
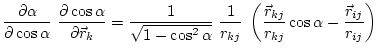 |
(6.20) | ||
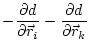 |
(6.21) |
These equations for the derivatives have a numerical instability when
the angle goes to 0 or to 180![]() .
Presently, the problem is `solved' by testing for the size
of the angle; if it is too small, the derivatives are set to 0
in the hope that other restraints will eventually pull the angle
towards well behaved regions. Thus, angle restraints of 0 or
180
.
Presently, the problem is `solved' by testing for the size
of the angle; if it is too small, the derivatives are set to 0
in the hope that other restraints will eventually pull the angle
towards well behaved regions. Thus, angle restraints of 0 or
180![]() should not be used in the conjugate gradients or molecular dynamics
optimizations.
should not be used in the conjugate gradients or molecular dynamics
optimizations.
Dihedral angle is defined by points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (
(![]() ):
):
| (6.22) |
| (6.23) |
The first derivatives of ![]() with respect to Cartesian coordinates are:
with respect to Cartesian coordinates are:
| (6.24) |
| (6.25) |
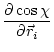 |
(6.26) | ||
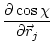 |
(6.27) | ||
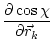 |
(6.28) | ||
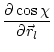 |
(6.29) | ||
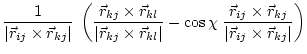 |
(6.30) | ||
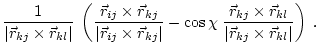 |
(6.31) |
These equations for the derivatives have a numerical instability when the angle goes to 0. Thus, the following set of equations is used instead [van Schaik et al., 1993]:
| (6.32) | |||
| (6.33) | |||
| (6.34) | |||
| (6.35) | |||
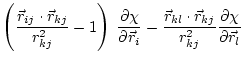 |
(6.36) | ||
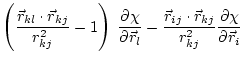 |
(6.37) |
The only possible instability in these equations is when the length of
the central bond of the dihedral, ![]() , goes to 0. In such a case,
which should not happen, the derivatives are set to 0. The expressions for
an improper dihedral angle, as opposed to a dihedral or dihedral angle,
are the same, except that indices
, goes to 0. In such a case,
which should not happen, the derivatives are set to 0. The expressions for
an improper dihedral angle, as opposed to a dihedral or dihedral angle,
are the same, except that indices ![]() are permuted to
are permuted to ![]() .
In both cases, covalent bonds
.
In both cases, covalent bonds ![]() ,
, ![]() , and
, and ![]() are defining
the angle.
are defining
the angle.
xx
Atomic density for a given atom is simply calculated as the number of atoms within a distance energy_data.contact_shell of that atom. First derivatives are not calculated, and are always returned as 0.
The absolute atomic coordinates ![]() ,
, ![]() and
and ![]() are available
for every point
are available
for every point ![]() , primarily for use in anchoring points to planes, lines
or points. Their first derivatives with respect to Cartesian coordinates
are of course simply 0 or 1.
, primarily for use in anchoring points to planes, lines
or points. Their first derivatives with respect to Cartesian coordinates
are of course simply 0 or 1.